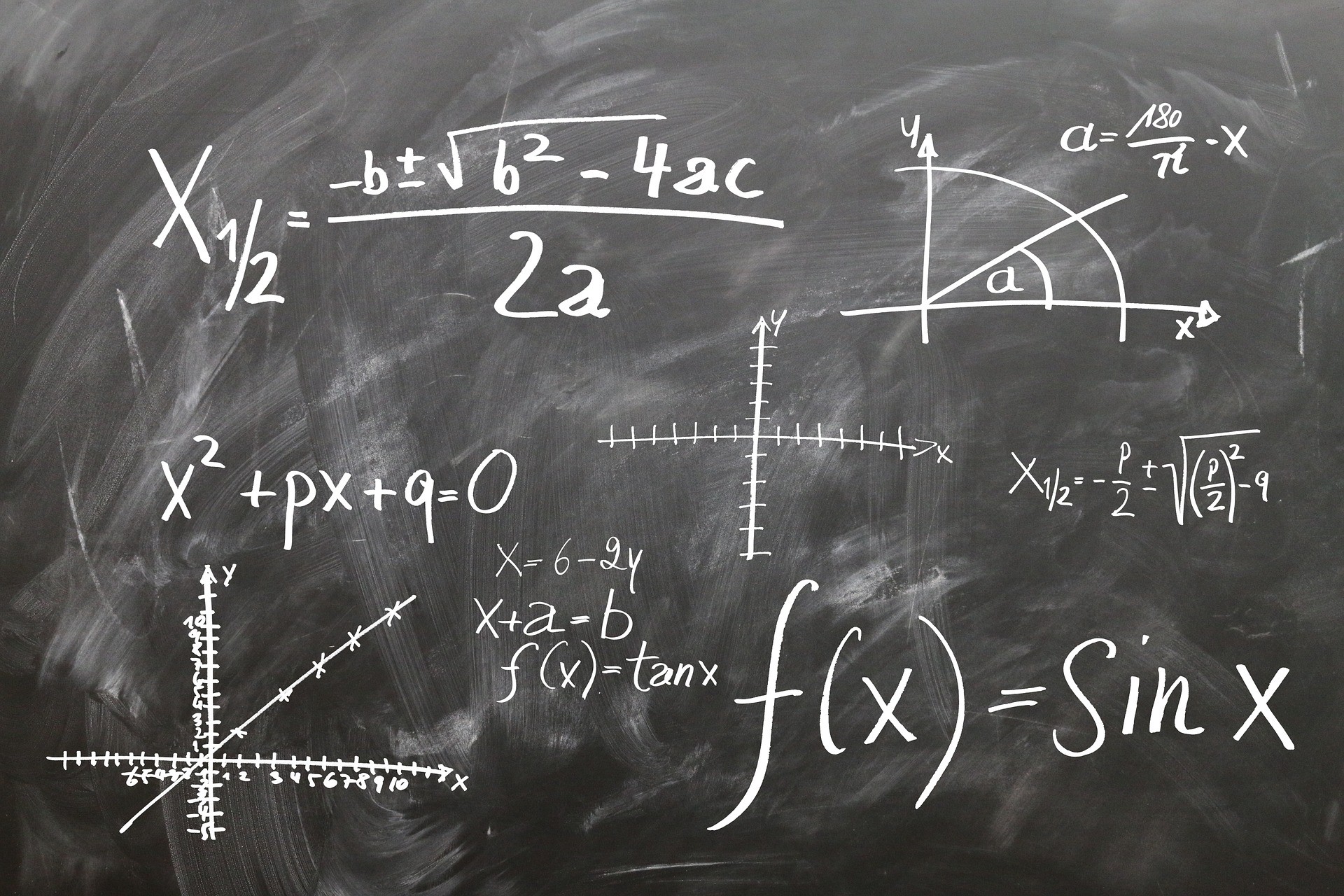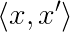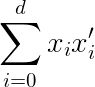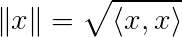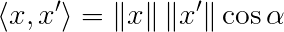Source:- towardsdatascience.com
Generally, in machine learning, we want to put similar things in similar places. This rule is universal to all of machine learning, be it supervised, unsupervised, classification, regression. The question is, how do we exactly determine what is similar? In order to shed light on the matter, we are going to start with the essential foundation for learning with kernels, the dot product.
The dot product between two vectors is an amazing thing. We can definitely say that it measures similarity in a sense. Normally, in machine learning literature the dot product is denoted by the following:
Denoting the dot product between the vectors x and x’. Note that for brevity sake I omitted the arrow for the vector notation. This notation is shorthand for the sum over the product of the vector components:
Coincidentally, the norm of the vector is the square root of the dot product with itself, denoted as:
This is of course not all there is to it. We also know the cosine rule that states that the dot product is equal to the cosine of the angle between the vectors multiplied their norms (this is easily provable by simple trigonometry):
The nice thing about talking about angles and norms is that we can now visualize what does this dot product mean. Let us draw these two vectors with and angle α between them:
So if we take the dot product as a measure of similarity. When is it going to be at its maximum? Meaning that the vectors are most similar. Obviously, this is going to happen when the cosine is equal to 1, which happens when the angle us 0 degrees or radians. If the vector’s respective norms are the same, then obviously we are talking about the same vector! Not bad. Let´s carve into stone what we learned so far:
The dot product is a measure of similarity between vectors.
Now you hopefully get why it is useful to talk about dot products.
Of course, the dot product as a measure of similarity can be useful in a problem or can be completely useless, depending on the problem you are trying to solve. Hence we need some kind of a transformation on our input space that is going to make the dot product actually useful as a measure of similarity. We denote this transformation with ϕ. Now, we can define the meaning of a kernel, the dot product in the mapped space:
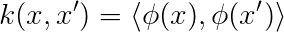
So the definition of the kernel is quite straight forward, a measure of similarity in the mapped space. The thing is, mathematicians, like to be concrete. There should be no implicit assumptions about the underlying functions and spaces that they deal with, hence there is quite a lot of theory behind kernels from functional analysis which needs another article or a few for that matter. In a nutshell, we need to explicitly state what kind of function do we want for ϕ:
We want a function that maps from our domain X to a space where the dot product is well defined, meaning that it is a good measure of similarity.
Kernels can be used as a generalization of any algorithm that can be defined in terms of dot products (or norms for that matter). The most famous examples of algorithms that use kernels as their backbone are Support Vector Machines and Gaussian Processes, but also there are examples of kernels being used with neural networks.
Another reason that we would effectively need kernels and the mapping function ϕ is that the input space may not have a well-defined dot product. Let us shortly study a case of document analysis where we simply want to derive the similarity between two documents based on their topic and then maybe cluster them. In this case, what is exactly the dot product between these two documents? One option is to take the ASCII code of the characters of the documents and concatenate them in a huge vector — of course, this is not something that you would do in practice but it is rather food for thought. It is nice that we have our documents defined as vectors now. But the problem remains regarding the length, i.e. different documents have different length. But no biggy, we may be able to solve this just by padding out the shorter document with an EOS character to a certain length. Then we can calculate a dot product in this high dimensional space. But, there is the question again of the relevance of this dot product or rather to say what does this dot product actually mean. Obviously, the slightest change in characters changes the dot product. Even if we exchange a word with its synonym it changes the dot product. This is something that you would want to avoid when comparing two documents topic-wise.
So how do kernels come into play here? Ideally, you would want to find a mapping function ϕ that maps your input space to a feature space where the dot product has the meaning that you want. In the case of document comparison, that the dot product is high for documents that are semantically similar. In other words, this mapping should make the job of your classifier easier in that the data becomes more easily separable.
We can look at the archetypical XOR example now to grasp the concept. The XOR function is a binary function and it looks something like this:
The blue points are classified as 0 and the red points are classified as 1. We can assume this is a noised XOR since the clusters have a big spread. We notice one thing straight off the bat, the data is not linearly separable. I.e. we cannot put a line between the red and blue points that separates all of them.
What can we do in this case? We can apply a specific mapping function that makes our job a lot easier. Concretely, let us construct a mapping function that is going to do a one-sided reflection of the input space around the line that passes through the red point clusters. We are going to reflect all of the points that lie under this line around the line. Our mapping function would have the following result:
After the mapping, our data becomes nicely linearly separable, so if we have a model that is trying to fit a separating hyperplane (as the perceptron for example), this is one of the ideal cases. Obviously, linear separability is a very nice thing to have. But in order to build efficient models, we do not necessarily need linear separability which means that not all mapping functions need to lead to linearly separable data in order to build efficient models.
Oftentimes people mix up the concepts of applying the kernel vs. applying the mapping function. The output of a kernel function is a scalar, a similarity or dissimilarity measure of two points. The output of the mapping function is a vector based on which we calculate the similarity. The funky thing about kernels is that we can sometimes calculate the dot product of the mapping in our original space, without needing to map the input explicitly. This allows us to deal with infinite dimensional mappings! That is quite a hard thing to grasp, so this I will leave for a later article.
For closing remarks I would like to recommend the book from Smola and Schoelkopf: Learning with Kernels. The book gives a comprehensive treatment of kernel machines and their theoretical background. Other than that, stay tuned for going even deeper into kernels!